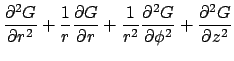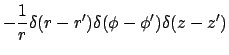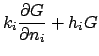

Next: GF, Double-Sum Form
Up: Solid Cylinder, Steady 3D,
Previous: Solid Cylinder, Steady 3D,
The steady Green's function represents the response at point 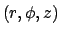 caused
by a point source of heat located at
caused
by a point source of heat located at
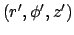 .
The GF associated with equation (1) satisfies the following equations:
.
The GF associated with equation (1) satisfies the following equations:
Note that the boundary conditions are homogeneous and of the same type
as the temperature
problem, Eq. (1). The volume energy generation is replaced by point
heat source described by a Dirac delta
function, 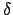 . Most of the quantities in this discussion have units:
. Most of the quantities in this discussion have units:
![$k=[W/m/K]$](img41.png) ;
; ![$h=[W/m^{2}/K]$](img42.png) ; and,
; and, ![$G=[meters]$](img43.png) for steady heat conduction in the cylinder.
for steady heat conduction in the cylinder.
Frank Pribyl
2005-06-07
![]() caused
by a point source of heat located at
caused
by a point source of heat located at
![]() .
The GF associated with equation (1) satisfies the following equations:
.
The GF associated with equation (1) satisfies the following equations: