Consider the steady temperature in the cylinder caused either by heating at
the boundaries or by internal energy generation. The temperature satisfies
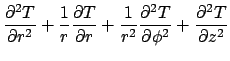 |
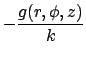 |
(1) | |
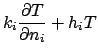 |
The temperature can be stated in the form of integrals with the method of
Green's functions. If the Green's function ![]() is known, then the
temperature that satisfies equation (1) is given by:
is known, then the
temperature that satisfies equation (1) is given by:
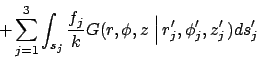
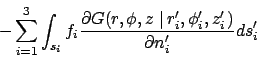 |
(2) |
The same Green's function appears in each integral but is evaluated at
locations appropriate for each integral. Here position
![]() is located on
surface
is located on
surface ![]() . Surface differential
. Surface differential ![]() is associated with appropriate
surfaces of the cylinder: on surface
is associated with appropriate
surfaces of the cylinder: on surface ![]() ,
,
![]() ; and,
at
; and,
at ![]() or
or ![]() ,
,
![]() . The two summations represent
all possible combinations of boundary conditions, but with only one type of
boundary condition on each of three surfaces of the cylinder. Mixed-type
boundary conditions are not treated.
. The two summations represent
all possible combinations of boundary conditions, but with only one type of
boundary condition on each of three surfaces of the cylinder. Mixed-type
boundary conditions are not treated.