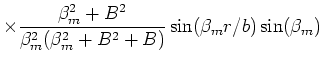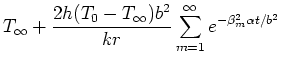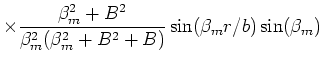

Next: Steady Temperature in a
Up: EXAMPLES, TEMPERATURE FROM GF
Previous: Solid cylinder with internal
Find the temperature in a solid sphere of radius 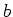 , initially at elevated
temperature
, initially at elevated
temperature 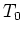 , that is suddenly immersed in a fluid at constant temperature
, that is suddenly immersed in a fluid at constant temperature
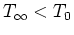 .
The heat transfer coefficient for the process is a constant value,
.
The heat transfer coefficient for the process is a constant value, 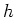 .
The temperature satisfies the following equations:
.
The temperature satisfies the following equations:
As stated, this is case RS03B1T1. Note that the convection boundary condition
provides
that the heat flux at 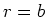 will be positive for
will be positive for
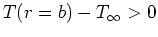 .
There are two driving terms, however one of them
can be made homogeneous by suitable choice of a normalized temperature.
(Generally it
is better to zero out boundary conditions in favor of initial conditions
but the purpose of this example is to demonstrate the convection boundary term.)
Let
.
There are two driving terms, however one of them
can be made homogeneous by suitable choice of a normalized temperature.
(Generally it
is better to zero out boundary conditions in favor of initial conditions
but the purpose of this example is to demonstrate the convection boundary term.)
Let
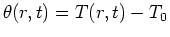 . Then the differential equation is unchanged,
the
initial condition is
. Then the differential equation is unchanged,
the
initial condition is
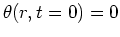 , and the boundary condition may be
written in standard form as
, and the boundary condition may be
written in standard form as
Where
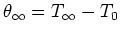 .
The temperature is given by the boundary-heating term of the GF solution
equation in the form
.
The temperature is given by the boundary-heating term of the GF solution
equation in the form
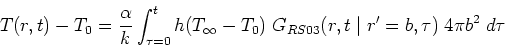 |
(27) |
The large-time GF for this case is given by:
where the eigenvalues are found from
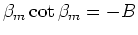 and where
and where
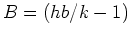 .
The time integral is easily evaluated to give
.
The time integral is easily evaluated to give
For numerical evaluation the steady-state term of the series should
be replaced by its constant value. As
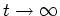 ,
the sphere takes on the fluid temperature. That is,
,
the sphere takes on the fluid temperature. That is,
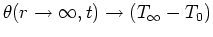 . Substitute this constant value in place of the
steady-state portion of the above series to find the following result:
. Substitute this constant value in place of the
steady-state portion of the above series to find the following result:
Note the sign change.


Next: Steady Temperature in a
Up: EXAMPLES, TEMPERATURE FROM GF
Previous: Solid cylinder with internal
2004-01-31
![]() , initially at elevated
temperature
, initially at elevated
temperature ![]() , that is suddenly immersed in a fluid at constant temperature
, that is suddenly immersed in a fluid at constant temperature
![]() .
The heat transfer coefficient for the process is a constant value,
.
The heat transfer coefficient for the process is a constant value, ![]() .
The temperature satisfies the following equations:
.
The temperature satisfies the following equations:
![$\displaystyle \frac{1}{r^2} \frac{\partial}{\partial r} \left[r^2 \frac{\partial T}
{\partial r} \right]$](img154.png)
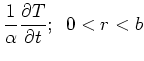
![$\displaystyle \left[ -k \frac{\partial T}{\partial r} \right]_{r=b}$](img155.png)
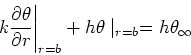
![$\displaystyle \frac{1}{2\pi b r r^{\prime}}
\sum_{m=1}^{\infty}\exp \left[ -\beta _{m}^{2}\alpha (t-\tau )/b^{2}\right]$](img164.png)
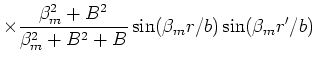
![$\displaystyle \frac{2h(T_{\infty}-T_0)b^2 }{kr} \sum_{m=1}^{\infty}
[1-e^{-\beta _{m}^{2}\alpha t/b^{2}}]$](img169.png)