

Next: Solid sphere with convection.
Up: EXAMPLES, TEMPERATURE FROM GF
Previous: 1D Slab heated at
A long cylinder is initially at zero temperature and the boundary at 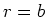 is maintained at zero temperature. Find the temperature in the cylinder
resulting from spatially uniform internal energy generation,
is maintained at zero temperature. Find the temperature in the cylinder
resulting from spatially uniform internal energy generation, 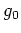 (W/m
(W/m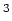 ).
).
The temperature satisfies the following equations:
This case is number R01B0T0G1. The GF solution equation for the temperature
contains only the internal heating term:
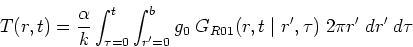 |
(19) |
The large-time form of the GF for this case is given by
where 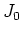 and
and 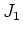 are Bessel functions and the eigenvalues given by
are Bessel functions and the eigenvalues given by
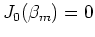 .
The two integrals in the above solution will be considered one at a time.
The spatial integral over
.
The two integrals in the above solution will be considered one at a time.
The spatial integral over 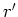 acts on one
acts on one 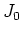 term, and it may
be simplified by the substitution
term, and it may
be simplified by the substitution
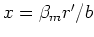 and then
evaluated as shown below:
and then
evaluated as shown below:
The time integral acts only on the exponential term of the series for the GF,
given by
![\begin{displaymath}
\int_{\tau=0}^t e^{-\beta _{m}^{2} \alpha (t-\tau )/b^2} \; ...
...= \frac{b^2}{\beta_m^2 \alpha}[1- e^{-\beta_m^2 \alpha t/b^2}]
\end{displaymath}](img137.png) |
(22) |
Then the above two integrals can be combined with the entire GF solution
to give:
![\begin{displaymath}
T(r,t)=2\frac{g_0b^2}{k} \sum_{m=1}^{\infty}
[1- e^{-\beta_m...
...t/b^2}] \frac{J_{0}( \beta_{m}r/b) }
{\beta_m^3 J_1(\beta_m) }
\end{displaymath}](img138.png) |
(23) |
For numerical evaluation, the steady term should be computed separately and
substituted for the slowly converging series term (the term without the
exponential).
When the steady-state portion of the solution is substituted (see below),
the temperature is given by:
![\begin{displaymath}
T(r,t)= \frac{g_0b^2}{4k} \left[ 1-(r/b)^2 \right] - 2\frac{...
... t/L^2} \frac{J_0 ( \beta _{m}r/b) }
{\beta_m^3 J_1(\beta_m) }
\end{displaymath}](img139.png) |
(24) |
This form of the solution converges rapidly for
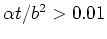 .
.
Steady Solution. Next the steady solution for the solid sphere
with internal heating will be derived. The steady temperature satisfies
the following differential equation:
The general solution may be found by integrating the differential equation twice:
The constants of integration 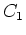 and
and 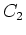 may be determined by applying the
boundary condtions. For
may be determined by applying the
boundary condtions. For 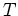 to be bounded at
to be bounded at 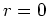 requires
requires 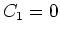 . At
. At 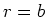 the boundary condition
the boundary condition 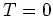 then determines
then determines 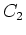 . Then the steady temperature
is given by
. Then the steady temperature
is given by


Next: Solid sphere with convection.
Up: EXAMPLES, TEMPERATURE FROM GF
Previous: 1D Slab heated at
2004-01-31
![]() is maintained at zero temperature. Find the temperature in the cylinder
resulting from spatially uniform internal energy generation,
is maintained at zero temperature. Find the temperature in the cylinder
resulting from spatially uniform internal energy generation, ![]() (W/m
(W/m![]() ).
).
![$\displaystyle \frac{1}{r} \frac{\partial}{\partial r} \left[r \frac{\partial T}{\partial r} \right]
+ \frac{g_0}{k}$](img118.png)
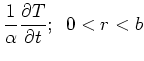
![$\displaystyle \frac{1}{\pi b^{2}} \sum_{m=1}^{\infty
}\exp \left[ -\beta _{m}^{2}\alpha (t-\tau )/b^{2}\right]$](img126.png)
![$\displaystyle \times \frac{J_{0}(\beta _{m}r/b) J_{0}(\beta _{m}r^{\prime }/b) } {\left[
J_{1}(\beta _{m}) \right] ^{2}}$](img127.png)
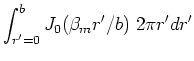
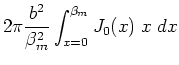
![$\displaystyle 2 \pi \frac{b^2}{\beta_m^2} \left[ x J_1(x) \right]_{x=0}^{\beta_m}$](img135.png)
![$\displaystyle 2 \pi \frac{b^2}{\beta_m^2} \left[ \beta_m J_1(\beta_m) -0 \right]$](img136.png)
![\begin{displaymath}
\int_{\tau=0}^t e^{-\beta _{m}^{2} \alpha (t-\tau )/b^2} \; ...
...= \frac{b^2}{\beta_m^2 \alpha}[1- e^{-\beta_m^2 \alpha t/b^2}]
\end{displaymath}](img137.png)
![\begin{displaymath}
T(r,t)=2\frac{g_0b^2}{k} \sum_{m=1}^{\infty}
[1- e^{-\beta_m...
...t/b^2}] \frac{J_{0}( \beta_{m}r/b) }
{\beta_m^3 J_1(\beta_m) }
\end{displaymath}](img138.png)
![\begin{displaymath}
T(r,t)= \frac{g_0b^2}{4k} \left[ 1-(r/b)^2 \right] - 2\frac{...
... t/L^2} \frac{J_0 ( \beta _{m}r/b) }
{\beta_m^3 J_1(\beta_m) }
\end{displaymath}](img139.png)
![$\displaystyle \frac{1}{r} \frac{\partial}{\partial r} \left[r \frac{\partial T}{\partial r} \right]$](img141.png)
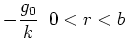
![\begin{displaymath}
T(r) = \frac{g_0 b^2}{4k} \left[ 1 - \frac{r^2}{b^2} \right]
\end{displaymath}](img150.png)