next up previous
Next: Helmholtz Equation: Steady-Periodic Up: Rectangular Coordinates. Helmholtz Equation. Previous: Semi infinite body, steady

Plate, steady 1-D Helmholtz.

X11 Plate, G = 0 (Dirichlet) at x = 0 and x = L.

GX11(x $\displaystyle \left\vert\vphantom{ \,x^{\prime }}\right.$ x$\scriptstyle \prime$$\displaystyle \left.\vphantom{ \,x^{\prime }}\right.$) = $\displaystyle \left\{\vphantom{ \begin{array}{cc}\sinh [m(L-x^{\prime })]\sin... ...]\sinh mx^{\prime }/(m\sinh mL) & \text{for }x>x^{\prime }\end{array}}\right.$$\displaystyle \begin{array}{cc}\sinh [m(L-x^{\prime })]\sinh mx/(m\sinh mL) & ... ...h [m(L-x)]\sinh mx^{\prime }/(m\sinh mL) & \text{for }x>x^{\prime }\end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{cc}\sinh [m(L-x^{\prime })]\sinh... ...]\sinh mx^{\prime }/(m\sinh mL) & \text{for }x>x^{\prime }\end{array}}\right.$    

X12 Plate, G = 0 (Dirichlet) at x = 0 and $ \partial$G/$ \partial$x = 0 (Neumann) at x = L.

GX12(x $\displaystyle \left\vert\vphantom{ \,x^{\prime }}\right.$ x$\scriptstyle \prime$$\displaystyle \left.\vphantom{ \,x^{\prime }}\right.$) = $\displaystyle \left\{\vphantom{ \begin{array}{cc}\cosh [m(L-x^{\prime })]\sin... ...]\sinh mx^{\prime }/(m\cosh mL) & \text{for }x>x^{\prime }\end{array}}\right.$$\displaystyle \begin{array}{cc}\cosh [m(L-x^{\prime })]\sinh mx/(m\cosh mL) & ... ...h [m(L-x)]\sinh mx^{\prime }/(m\cosh mL) & \text{for }x>x^{\prime }\end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{cc}\cosh [m(L-x^{\prime })]\sinh... ...]\sinh mx^{\prime }/(m\cosh mL) & \text{for }x>x^{\prime }\end{array}}\right.$    

X13 Plate, G = 0 (Dirichlet) at x = 0 and k$ \partial$G/$ \partial$x + hG = 0 (Neumann) at x = L. Note where B2 = h2L/k

GX13(x $\displaystyle \left\vert\vphantom{ \,x^{\prime }}\right.$ x$\scriptstyle \prime$$\displaystyle \left.\vphantom{ \,x^{\prime }}\right.$) = $\displaystyle \left\{\vphantom{ \begin{array}{c}\frac{1}{m}[\cosh m(L-x^{\pri... ...\frac{B_{2}}{mL}\sinh mL]\text{; \space for }x>x^{\prime }\end{array}}\right.$$\displaystyle \begin{array}{c}\frac{1}{m}[\cosh m(L-x^{\prime })+\frac{B_{2}}{... ...\cosh mL+\frac{B_{2}}{mL}\sinh mL]\text{; \space for }x>x^{\prime }\end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{c}\frac{1}{m}[\cosh m(L-x^{\prim... ...\frac{B_{2}}{mL}\sinh mL]\text{; \space for }x>x^{\prime }\end{array}}\right.$    

X21 Plate, $ \partial$G/$ \partial$x = 0 (Neumann) at x = 0 and G = 0 (Dirichlet) at x = L.

GX21(x $\displaystyle \left\vert\vphantom{ \,x^{\prime }}\right.$ x$\scriptstyle \prime$$\displaystyle \left.\vphantom{ \,x^{\prime }}\right.$) = $\displaystyle \left\{\vphantom{ \begin{array}{cc}\cosh (mx)\sinh [m(L-x^{\pri... ...m(L-x^{\prime })]/(m\cosh mL) & \text{for }x>x^{\prime }\end{array}}\right.$$\displaystyle \begin{array}{cc}\cosh (mx)\sinh [m(L-x^{\prime })]/(m\cosh mL) ... ...})\sinh [m(L-x^{\prime })]/(m\cosh mL) & \text{for }x>x^{\prime }\end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{cc}\cosh (mx)\sinh [m(L-x^{\prim... ...m(L-x^{\prime })]/(m\cosh mL) & \text{for }x>x^{\prime }\end{array}}\right.$    


X22 Plate, $ \partial$G/$ \partial$x = 0 (Neumann) at both sides.

GX22(x $\displaystyle \left\vert\vphantom{ \,x^{\prime }}\right.$ x$\scriptstyle \prime$$\displaystyle \left.\vphantom{ \,x^{\prime }}\right.$) = $\displaystyle \left\{\vphantom{ \begin{array}{cc}\cosh (mx)\cosh [m(L-x^{\pri... ...me })\cosh [m(L-x)]/(m\sinh mL) & \text{for }x>x^{\prime }\end{array}}\right.$$\displaystyle \begin{array}{cc}\cosh (mx)\cosh [m(L-x^{\prime })]/(m\sinh mL) ... ...(mx^{\prime })\cosh [m(L-x)]/(m\sinh mL) & \text{for }x>x^{\prime }\end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{cc}\cosh (mx)\cosh [m(L-x^{\prim... ...me })\cosh [m(L-x)]/(m\sinh mL) & \text{for }x>x^{\prime }\end{array}}\right.$    

X23 Plate, $ \partial$G/$ \partial$x = 0 (Neumann) at x = 0 and k$ \partial$G/$ \partial$x + h2G = 0 (convection) at x = L.

GX23(x $\displaystyle \left\vert\vphantom{ \,x^{\prime }}\right.$ x$\scriptstyle \prime$$\displaystyle \left.\vphantom{ \,x^{\prime }}\right.$) = same asGX32(x $\displaystyle \left\vert\vphantom{ \,x^{\prime }}\right.$ x$\scriptstyle \prime$$\displaystyle \left.\vphantom{ \,x^{\prime }}\right.$) with $\displaystyle \left\{\vphantom{ \begin{array}{c}x\rightarrow L-x \\ x^{\prime }\rightarrow L-x^{\prime }\end{array}}\right.$$\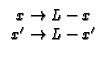displaystyle \begin{array}{c}x\rightarrow L-x \\ x^{\prime }\rightarrow L-x^{\prime }\end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{c}x\rightarrow L-x \\ x^{\prime }\rightarrow L-x^{\prime }\end{array}}\right.$    


    For  x < x$\scriptstyle \prime$, GX23(x $\displaystyle \left\vert\vphantom{ \,x^{\prime }}\right.$ x$\scriptstyle \prime$$\displaystyle \left.\vphantom{ \,x^{\prime }}\right.$) =  
    $\displaystyle {\frac{(mL+B_{2})\left[ e^{m(x^{\prime }-x+2L)}+e^{m(2L-x-x^{\pri... ...mL-B_{2})2e^{m(x^{\prime }-x)}}{2m\left[ (mL+B_{2})e^{2mL}-(mL-B_{2})\right] }}$  
       
    For  x < x$\scriptstyle \prime$, GX23(x $\displaystyle \left\vert\vphantom{ \,x^{\prime }}\right.$ x$\scriptstyle \prime$$\displaystyle \left.\vphantom{ \,x^{\prime }}\right.$) =  
    $\displaystyle {\frac{(mL+B_{2})\left[ e^{m(x-x^{\prime }+2L)}+e^{m(2L-x-x^{\pri... ...mL-B_{2})2e^{m(x-x^{\prime })}}{2m\left[ (mL+B_{2})e^{2mL}-(mL-B_{2})\right] }}$  


X31 Plate, - k$ \partial$G/$ \partial$x + h1G = 0 (convection) at x = 0 and $ \partial$G/$ \partial$x = 0 (Neumann) at x = L. Note B1 = h1L/k.



    For  x < x$\scriptstyle \prime$, GX31(x $\displaystyle \left\vert\vphantom{ \,x^{\prime }}\right.$ x$\scriptstyle \prime$$\displaystyle \left.\vphantom{ \,x^{\prime }}\right.$) =  
    $\displaystyle {\frac{(mL+B_{1})\left[ e^{m(x-x^{\prime }+2L)}-e^{m(x+x^{\prime ... ...}-e^{m(x-x^{\prime })}\right] }{2m% \left[ (mL+B_{1})e^{2mL}+mL-B_{1}\right] }}$  
       
    For  x < x$\scriptstyle \prime$, GX31(x $\displaystyle \left\vert\vphantom{ \,x^{\prime }}\right.$ x$\scriptstyle \prime$$\displaystyle \left.\vphantom{ \,x^{\prime }}\right.$) =  
    $\displaystyle {\frac{(mL+B_{1})\left[ e^{m(x^{\prime }-x+2L)}-e^{m(x+x^{\prime ... ...}-e^{m(x^{\prime }-x)}\right] }{2m% \left[ (mL+B_{1})e^{2mL}+mL-B_{1}\right] }}$  

X32 Plate, - k$ \partial$G/$ \partial$x + hG = 0 (convection) at x = 0 and $ \partial$G/$ \partial$x = 0 (Neumann) at x = L. Note B1 = h1L/k .



    For  x < x$\scriptstyle \prime$, GX32(x $\displaystyle \left\vert\vphantom{ \,x^{\prime }}\right.$ x$\scriptstyle \prime$$\displaystyle \left.\vphantom{ \,x^{\prime }}\right.$) =  
    $\displaystyle {\frac{(mL+B_{1})\left[ e^{m(x-x^{\prime }+2L)}+e^{m(x+x^{\prime ... ...e^{m(x-x^{\prime })}\right] }{2m% \left[ (mL+B_{1})e^{2mL}-(mL-B_{1})\right] }}$  
       
    For  x < x$\scriptstyle \prime$, GX32(x $\displaystyle \left\vert\vphantom{ \,x^{\prime }}\right.$ x$\scriptstyle \prime$$\displaystyle \left.\vphantom{ \,x^{\prime }}\right.$) =  
    $\displaystyle {\frac{(mL+B_{1})\left[ e^{m(x^{\prime }-x+2L)}+e^{m(x+x^{\prime ... ...e^{m(x^{\prime }-x)}\right] }{2m% \left[ (mL+B_{1})e^{2mL}-(mL-B_{1})\right] }}$  

X33 Plate, - k$ \partial$G/$ \partial$x + h1G = 0 (convection) at x = 0 and k$ \partial$G/$ \partial$x + h2G = 0 (convection) at x = L. Note B1 = h1L/k and B2 = h2L/k.
For x < x$\scriptstyle \prime$, GX33(x $\displaystyle \left\vert\vphantom{ \,x^{\prime }}\right.$ x$\scriptstyle \prime$$\displaystyle \left.\vphantom{ \,x^{\prime }}\right.$) =  
$\displaystyle {\frac{1}{2m}}$   x $\displaystyle \left[\vphantom{ (m^{2}L^{2}+B_{1}mL-B_{2}mL-B_{1}B_{2})e^{m(x+x^{\prime })}}\right.$(m2L2 + B1mL - B2mL - B1B2)em(x + x$\scriptscriptstyle \prime$)$\displaystyle \left.\vphantom{ (m^{2}L^{2}+B_{1}mL-B_{2}mL-B_{1}B_{2})e^{m(x+x^{\prime })}}\right.$  
    + (m2L2 + B1mL + B2mL + B1B2)em(x - x$\scriptscriptstyle \prime$ + 2L)  
    + (m2L2 + B1mL - B2mL + B1B2)e-m(x - x$\scriptscriptstyle \prime$)  
    $\displaystyle \left.\vphantom{ +(m^{2}L^{2}-B_{1}mL+B_{2}mL-B_{1}B_{2})e^{-m(x+x^{\prime }-2L)} }\right.$ + (m2L2 - B1mL + B2mL - B1B2)e-m(x + x$\scriptscriptstyle \prime$ - 2L)$\displaystyle \left.\vphantom{ +(m^{2}L^{2}-B_{1}mL+B_{2}mL-B_{1}B_{2})e^{-m(x+x^{\prime }-2L)} }\right]$  
    ÷ $\displaystyle \left[\vphantom{ Qe^{2mL}-m^{2}L^{2}+B_{1}mL+B_{2}mL-B_{1}B_{2}}\right.$Qe2mL - m2L2 + B1mL + B2mL - B1B2$\displaystyle \left.\vphantom{ Qe^{2mL}-m^{2}L^{2}+B_{1}mL+B_{2}mL-B_{1}B_{2}}\right]$  
For x > x$\scriptstyle \prime$, GX33(x $\displaystyle \left\vert\vphantom{ \,x^{\prime }}\right.$ x$\scriptstyle \prime$$\displaystyle \left.\vphantom{ \,x^{\prime }}\right.$) =  
$\displaystyle {\frac{1}{2m}}$   x $\displaystyle \left[\vphantom{ (m^{2}L^{2}+B_{1}mL-B_{2}mL-B_{1}B_{2})e^{m(x+x^{\prime })}}\right.$(m2L2 + B1mL - B2mL - B1B2)em(x + x$\scriptscriptstyle \prime$)$\displaystyle \left.\vphantom{ (m^{2}L^{2}+B_{1}mL-B_{2}mL-B_{1}B_{2})e^{m(x+x^{\prime })}}\right.$  
    + (m2L2 + B1mL + B2mL + B1B2)em(x$\scriptscriptstyle \prime$ - x + 2L)  
    + (m2L2 + B1mL - B2mL + B1B2)e-m(x$\scriptscriptstyle \prime$ - x)  
    $\displaystyle \left.\vphantom{ +(m^{2}L^{2}-B_{1}mL+B_{2}mL-B_{1}B_{2})e^{-m(x+x^{\prime }-2L)} }\right.$ + (m2L2 - B1mL + B2mL - B1B2)e-m(x + x$\scriptscriptstyle \prime$ - 2L)$\displaystyle \left.\vphantom{ +(m^{2}L^{2}-B_{1}mL+B_{2}mL-B_{1}B_{2})e^{-m(x+x^{\prime }-2L)} }\right]$  
    ÷ $\displaystyle \left[\vphantom{ Qe^{2mL}-m^{2}L^{2}+B_{1}mL+B_{2}mL-B_{1}B_{2}}\right.$Qe2mL - m2L2 + B1mL + B2mL - B1B2$\displaystyle \left.\vphantom{ Qe^{2mL}-m^{2}L^{2}+B_{1}mL+B_{2}mL-B_{1}B_{2}}\right]$  

where Q = (m2L2 + B1mL + B2mL + B1B2).
next up previous
Next: Helmholtz Equation: Steady-Periodic Up: Rectangular Coordinates. Helmholtz Equation. Previous: Semi infinite body, steady
Kevin D. Cole
2002-12-31