

Next: Plate, steady 1-D Helmholtz.
Up: Rectangular Coordinates. Helmholtz Equation.
Previous: Infinite body,rectangular coordinate, steady
X10 Semi-infinite body,
0 < x < 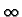 , with G = 0
(Dirichlet) at x = 0.
, with G = 0
(Dirichlet) at x = 0.
X20 Semi-infinite body,
0 < x < 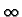 , with
, with
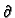 G/
G/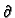 x = 0 at x=0.
x = 0 at x=0.
X30 Semi-infinite body,
0 < x < 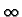 , with
- k
, with
- k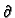 G/
G/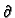 x + hG = 0 (convection) at x = 0. Note that B = h/(km).
x + hG = 0 (convection) at x = 0. Note that B = h/(km).
Kevin D. Cole
2002-12-31
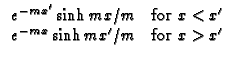
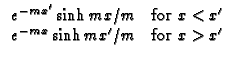
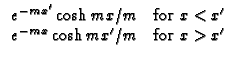
![$\displaystyle \begin{array}{cc}
\begin{array}{c}
\left[ e^{-m(x^{\prime }-x)}+\...
...}{1+B}e^{-m(x+x^{\prime })}\right]
/(2m) & \text{for }x>x^{\prime }
\end{array}$](img629.gif)