| = | - |
(8) | |
| 0 < x < L; 0 < y < W | |||
| ki |
= | 0 for faces i = 1, 2,..., 4 |
| = | - |
(8) | |
| 0 < x < L; 0 < y < W | |||
| ki |
= | 0 for faces i = 1, 2,..., 4 |
| G2D(x, y |
= | 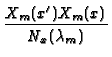 |
|
| x | 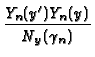 x
x 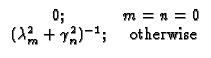
|
(9) |
G2D(x, y 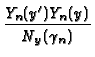 Pn(x, x Pn(x, x |
(10) |
| Pn(x, x |
= | {S1-S2-exp[- |
(11) |
| + S1+S2-exp[- |
|||
| + S1+S2+exp[- |
|||
| + S1-S2+exp[- |
|||
| ÷ | {2 |
| geometry | S1+ | S1- | S2+ | S2- |
| X11 | 1 | -1 | 1 | -1 |
| X12 | 1 | -1 | 1 | 1 |
| X13 | 1 | -1 |
|
|
| X21 | 1 | 1 | 1 | -1 |
| X22 | 1 | 1 | 1 | 1 |
| X23 | 1 | 1 |
|
|
| X31 |
|
|
1 | -1 |
| X32 |
|
|
1 | 1 |
| X33 |
|
|
|
|