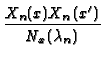| Case |
Range |
1D steady GF; units are meters. |
| X11 |
x > x |
x (1 - x/L) (1 - x/L) |
| |
x < x |
x(1 - x /L) /L) |
| X12 |
x > x |
x |
| |
x < x |
x |
| X13 |
x > x |
x [1 - B2(x/L)/(1 + B2)] [1 - B2(x/L)/(1 + B2)] |
| |
x < x |
x[1 - B2(x /L)/(1 + B2)] /L)/(1 + B2)] |
| X21 |
x > x |
L - x |
| |
x < x |
L - x |
| X22 * |
x > x |
(
x 2 + (x)2)/(2L) - x + L/3 2 + (x)2)/(2L) - x + L/3 |
| |
x < x |
(
x2 + (x 2)2)/(2L) - x 2)2)/(2L) - x + L/3 + L/3 |
| X23 |
x > x |
L(1 + 1/B2 - x/L) |
| |
x < x |
L(1 + 1/B2 - x /L) /L) |
| X31 |
x > x |
(B1x - B1x - B1x x/L + L - x)/(1 + B1) x/L + L - x)/(1 + B1) |
| |
x < x |
(B1x - B1xx /L + L - x /L + L - x )/(1 + B1) )/(1 + B1) |
| X32 |
x > x |
L(1/B1 + x /L) /L) |
| |
x < x |
L(1/B1 + x/L) |
| X33 |
x > x |
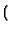 B1B2x B1B2x + B1x + B1x - B1B2x - B1B2x x/L - B2x + B2L + L x/L - B2x + B2L + L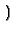 |
| |
|
÷ (B1B2 + B1 + B2) |
| |
x < x |
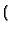 B1B2x + B1x - B1B2x B1B2x + B1x - B1B2x x/L - B2x x/L - B2x + B2L + L + B2L + L |
| |
|
÷ (B1B2 + B1 + B2) |