

Next: Infinite body, spherical coordinate,
Up: Heat Equation. Transient Heat
Previous: Hollow cylinder, transient 1-D.
The Heat Equation for transient 1-D Green's Functions in radial-spherical
coordinates is:
The radial-spherical Dirac delta function
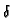 (r - r
(r - r ) has vector arguments and has units of [
meters-3].
) has vector arguments and has units of [
meters-3].
Kevin D. Cole
2002-12-31