

Next: Semi-infinite body heated at
Up: EXAMPLES, TEMPERATURE FROM GF
Previous: EXAMPLES, TEMPERATURE FROM GF
Consider the temperature caused by a spatially-varying initial condition in an
infinite 1D body. The temperature satisfies the following equations:
This case has number X00T5. The solution for the temperature is
given by the initial condition term of the GF solution equation:
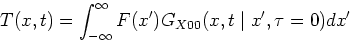 |
(2) |
Because the initial condition is zero over most of the domain the integral
may be carried out over the non-zero portion:
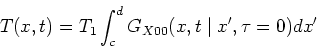 |
(3) |
Using the X00 Green's function evaluated at 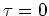 ,
,
![\begin{displaymath}
T(x,t) = T_1 \int_c^d [4 \pi \alpha t]^{-1/2}\exp \left[
-\frac{(x-x^{\prime })^{2}}{4 \alpha t}\right] dx^{\prime}
\end{displaymath}](img76.png) |
(4) |
Using the substitution
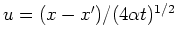 this
integral can be written as
this
integral can be written as
where the error function is defined
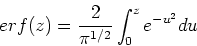 |
(7) |


Next: Semi-infinite body heated at
Up: EXAMPLES, TEMPERATURE FROM GF
Previous: EXAMPLES, TEMPERATURE FROM GF
2004-01-31
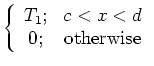
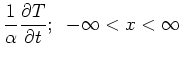
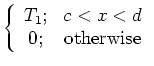
![\begin{displaymath}
T(x,t) = T_1 \int_c^d [4 \pi \alpha t]^{-1/2}\exp \left[
-\frac{(x-x^{\prime })^{2}}{4 \alpha t}\right] dx^{\prime}
\end{displaymath}](img76.png)
![$\displaystyle \frac{T_1}{\pi^{1/2} } \int_{(x-d)/[(4 \alpha t)^{1/2}]}
^{(x-c)/[(4 \alpha t)^{1/2}]}
e^{-u^2} du$](img79.png)
![$\displaystyle \frac{T_1}{2} \left\{ erf \left[ \frac{(x-c)}{(4 \alpha t)^{1/2}}
\right] - erf \left[ \frac{(x-d)}{(4 \alpha t)^{1/2}} \right] \right\}$](img80.png)