

Next: Helmholtz Equation. Steady with
Up: Radial-spherical coordinates. Steady 1-D
Previous: Solid sphere,steady 1-D.
RS11 Hollow sphere,
a 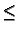 r
r 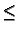 b, with G = 0
(Dirichlet) at r = a and at r = b.
RS12 Hollow sphere,
a
b, with G = 0
(Dirichlet) at r = a and at r = b.
RS12 Hollow sphere,
a 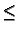 r
r 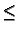 b, with G = 0
(Dirichlet) at r = a and
b, with G = 0
(Dirichlet) at r = a and
 G/
G/ r = 0 (Neumann) at r = b.
RS13 Hollow sphere,
a
r = 0 (Neumann) at r = b.
RS13 Hollow sphere,
a 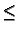 r
r 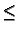 b, with G = 0
(Dirichlet) at r = 0 and
k
b, with G = 0
(Dirichlet) at r = 0 and
k G/
G/ r + h2G = 0 (convection) at r = b. Note
B2 = h2b/k.
RS21 Hollow sphere,
a
r + h2G = 0 (convection) at r = b. Note
B2 = h2b/k.
RS21 Hollow sphere,
a 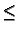 r
r 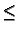 b, with
b, with
 G/
G/ r = 0 (Neumann) at r = a and G = 0 (Dirichlet) at r = b.
RS22 Hollow sphere,
a
r = 0 (Neumann) at r = a and G = 0 (Dirichlet) at r = b.
RS22 Hollow sphere,
a 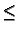 r
r 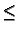 b, with
b, with
 G/
G/ r = 0 (Neumann) at both boundaries. Note that this geometry
requires a pseudo GF, denoted H. The temperature solution found from a
pseudo GF requires that the total volumetric heat flow is equal to the
boundary heat flow, and the spatial average temperature in the body must be
supplied as a known condition.
RS23 Hollow sphere,
a
r = 0 (Neumann) at both boundaries. Note that this geometry
requires a pseudo GF, denoted H. The temperature solution found from a
pseudo GF requires that the total volumetric heat flow is equal to the
boundary heat flow, and the spatial average temperature in the body must be
supplied as a known condition.
RS23 Hollow sphere,
a 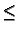 r
r 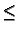 b, with
b, with
 G/
G/ r = 0 (Neumann) at r = a and
k
r = 0 (Neumann) at r = a and
k G/
G/ r + h2G = 0
(convection) at r = b. Note
B2 = h2b/k.
RS31 Hollow sphere,
a
r + h2G = 0
(convection) at r = b. Note
B2 = h2b/k.
RS31 Hollow sphere,
a 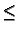 r
r 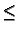 b, with
- k
b, with
- k G/
G/ r + h2G = 0 (convection) at r = a and G = 0 (Dirichlet) at r = b.
Note
B1 = h1a/k.
RS32 Hollow sphere,
a
r + h2G = 0 (convection) at r = a and G = 0 (Dirichlet) at r = b.
Note
B1 = h1a/k.
RS32 Hollow sphere,
a 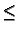 r
r 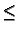 b, with
- k
b, with
- k G/
G/ r + h2G = 0 (convection) at r = a and
r + h2G = 0 (convection) at r = a and
 G/
G/ r = 0
(Neumann) at r = b. Note
B1 = h1a/k.
RS33 Hollow sphere,
a
r = 0
(Neumann) at r = b. Note
B1 = h1a/k.
RS33 Hollow sphere,
a 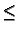 r
r 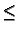 b, with
- k
b, with
- k G/
G/ r + h1G = 0 (convection) at r = a and
k
r + h1G = 0 (convection) at r = a and
k G/
G/ r + h2G = 0 (convection) at r = b. Note
B1 = h1a/k and
B2 = h2b/k.
r + h2G = 0 (convection) at r = b. Note
B1 = h1a/k and
B2 = h2b/k.


Next: Helmholtz Equation. Steady with
Up: Radial-spherical coordinates. Steady 1-D
Previous: Solid sphere,steady 1-D.
Kevin D. Cole
2002-12-31
![$\displaystyle \begin{array}{cc}
(b-r^{\prime })(1-a/r)/[r^{\prime }(b-a)] & \t...
...
& \\
(b-r)(1-a/r^{\prime })/[r(b-a)] & \text{for }r>r^{\prime }
\end{array}$](img596.gif)
![$\displaystyle \begin{array}{cc}
(b-r^{\prime })(1-a/r)/[r^{\prime }(b-a)] & \t...
...
& \\
(b-r)(1-a/r^{\prime })/[r(b-a)] & \text{for }r>r^{\prime }
\end{array}$](img596.gif)
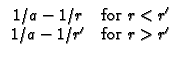
![$\displaystyle \begin{array}{c}
\lbrack B_{2}(\frac{a}{r}-\frac{ba}{rr^{\prime ...
...prime }}+1] \\
\div (B_{2}a-B_{2}b-a);\;\text{for }r>r^{\prime }
\end{array}$](img602.gif)
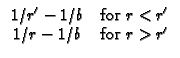
![$\displaystyle \begin{array}{cc}
\lbrack r^{2}/2+\left( r^{\prime }\right) ^{2}...
...{3}/r^{\prime
}+b^{3}/r]/(b^{3}-a^{3}) & \text{for }r>r^{\prime }
\end{array}$](img605.gif)
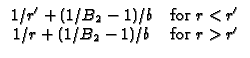
![$\displaystyle \begin{array}{c}
\lbrack B_{1}\frac{ba}{rr^{\prime }}-B_{1}\frac...
...r}+B_{1}+1] \\
\div (B_{1}b-B_{1}a+b);\;\text{for }r>r^{\prime }
\end{array}$](img611.gif)
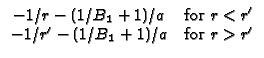
![$\displaystyle \begin{array}{c}
\lbrack B_{1}(\frac{a}{r}+1)+B_{1}B_{2}(1-\frac...
... \lbrack B_{2}b+B_{1}a+B_{1}B_{2}(b-a)];\;\text{for }r>r^{\prime }
\end{array}$](img617.gif)