

Next: Radial-Cylindrical Coordinates. Steady 1-D.
Up: Laplace Equation. Steady Heat
Previous: Pseudo GF. Rectangular coordinate,
by K. D. Cole and D. H. Y. Yen
The GF for the 2D strip satisfies:
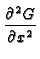 +
+ 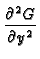 = -
= - 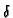 (x - x (x - x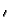 ) )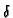 (y - y (y - y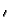 ) ) |
(18) |
Figure:
Geometry of (a) infinite and (b) semi-infinite strip.
![\includegraphics[height=4cm]{gfsemi_1.ps}](img510.gif) |
For the infinite strip, shown in Fig. 1a, the domain is
(- 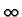 < x <
< x <  , 0 < y < W) and the boundary conditions are
, 0 < y < W) and the boundary conditions are
ki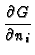 + hiG = 0
+ hiG = 0 |
|
at y = 0 and y = W |
|
G, 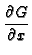 are bounded
are bounded |
|
as x 
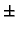
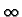 |
(19) |
For the semi-infinite strip, shown in Fig. 1b, the domain is
(0 < x < 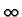 , 0 < y < W)and the homogeneous boundary conditions are
, 0 < y < W)and the homogeneous boundary conditions are
ki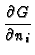 + hiG = 0
+ hiG = 0 |
|
at x = 0, y = 0, and y = W |
|
G, 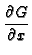 are bounded
are bounded |
|
as x 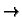 +
+  |
(20) |
The GF of infinite and semi-infinite strip are described by number XI0YKL
which represents 36 different GF for I = 0, 1, 2, or 3 and K, L =
1, 2, or 3. Note that the GF for I = 0 are for the infinite strip
geometry only.
The GF for the strip has a single-summation form with
eigenfunction Yn, eigenvalue
 , norm
Ny, and kernel function Pn, as follows:
, norm
Ny, and kernel function Pn, as follows:
G(x, y 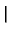 x x , y , y  ) = ) = 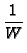 P0(x, x P0(x, x ) + ) + 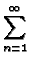 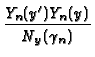 Pn(x, x Pn(x, x ) ) |
(21) |
The first term with kernel function P0 is needed only when
Y22 is part of the GF number (i.e., when zero is an eigenvalue).
There are nine different eigenfunctions associated with the nine
possible boundary condition combinations YKL (K, L = 1, 2, or 3).
Table 1 contains the eigenfunctions and norms, and Table 2
contains the associated eigenconditions (and eigenvalues for
simple cases).
Kernel functions Pn for n  0 are given by
0 are given by
Pn(x, x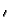 ) = ) = 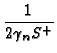 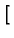 S+exp(- S+exp(- 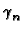 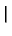 x - x x - x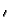 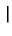 ) + S-exp(- ) + S-exp(- 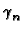 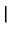 x + x x + x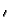 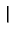 ) )![$\displaystyle \left.\vphantom{ S^{+}\exp(-\gamma _{n}\left\vert x-x^{\prime }\right\vert )+S^{-}\exp (-\gamma_{n}\left\vert x+x^{\prime }\right\vert )}\right]$](img520.gif) |
(22) |
where the values for S+ and S- are given in Table 3.
Kernel functions Pn for n 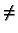 0 have four different forms,
one for each of the boundary condition combinations XI0 for I = 0,
1, 2, and 3.
0 have four different forms,
one for each of the boundary condition combinations XI0 for I = 0,
1, 2, and 3.
Kernel functions P0 satisfy
as well as appropriate homogeneous boundary conditions.
Functions P0, listed in Table 4, must be included in the GF
whenever zero is an eigenvalue (XI0Y22 for I = 0, 1, 2, and 3).
Table 1. Eigenfunctions and inverse norm a, b
| Geometry |
Yn(y) |
Ny-1 |
| Y11 |
sin( y) y) |
2/W |
| Y12 |
sin( y) y) |
2/W |
| Y13 |
sin( y) y) |
2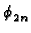 /W /W |
| Y21 |
cos( y) y) |
2/W |
| Y22 |
cos( y); y);
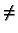 0
0 |
2/W for 
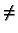 0
0 |
| |
1; = 0
= 0 |
1/W for  = 0
= 0 |
| Y23 |
cos( y) y) |
2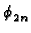 /W /W |
| Y31 |
 Wcos( Wcos( y) + (h1W/k)sin( y) + (h1W/k)sin( y) y) |
2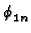 /W /W |
| Y32 |
 Wcos( Wcos( y) + (h1W/k)sin( y) + (h1W/k)sin( y) y) |
2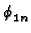 /W /W |
| Y33 |
 Wcos( Wcos( y) + (h1W/k)sin( y) + (h1W/k)sin( y) y) |
2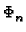 /W /W |
a Index
n = 1, 2,... for all cases except
Y22 with
n = 0, 1, 2,...
b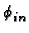 = [(
= [( W)2 + (hiW/k)2] ÷ [(
W)2 + (hiW/k)2] ÷ [( W)2 + (hiW/k)2 + hiW/k]
W)2 + (hiW/k)2 + hiW/k]
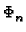 =
= 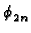 ÷ [(
÷ [( W)2 + (hiW/k)2 + (h1W/k)
W)2 + (hiW/k)2 + (h1W/k)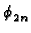 ]
]
Table 2. Eigencondition and eigenvalues for
Yn(y)a
| Geometry |
Eigencondition |
Eigenvalues |
| Y11 |
sin( W) = 0 W) = 0 |
n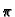 /W /W |
| Y12 |
cos( W) = 0 W) = 0 |
(2n - 1)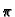 /2W /2W |
| Y13 |
 Wcot( Wcot( W) = - h2W/k W) = - h2W/k |
|
| Y21 |
cos( W) = 0 W) = 0 |
(2n - 1)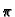 /2W /2W |
| Y22 |
sin( W) = 0 W) = 0 |
n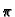 /W, n = 0, 1, 2,... /W, n = 0, 1, 2,... |
| Y23 |
 Wtan( Wtan( W) = h2W/k W) = h2W/k |
|
| Y31 |
 Wcot( Wcot( W) = - h1W/k W) = - h1W/k |
|
| Y32 |
 Wtan( Wtan( W) = hW/k W) = hW/k |
|
| Y33 |
tan( W) = [ W) = [ (h1 + h2)/k]/[ (h1 + h2)/k]/[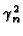 - h1h2k-2]
- h1h2k-2] |
|
a Index
n = 1, 2,... for all cases except
Y22 with
n = 0, 1, 2,...
Table 3. Coefficients for Pn for n 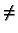 0, strip and semi-strip.
0, strip and semi-strip.
| Geometry |
S+ |
S- |
| X00 |
1 |
0 |
| X10 |
1 |
-1 |
| X20 |
1 |
1 |
| X30 |
 W + hW/k W + hW/k |
 W - hW/k W - hW/k |
Table 4. Kernel function P0 for strip and semi-strip.
| Geometry |
P0(x, x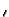 ) ) |
| X00 |
- 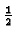 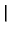 x - x x - x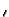 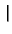 |
| X10 |
- 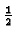 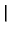 x - x x - x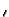 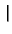 +
+ 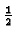 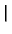 x + x x + x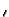 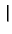 |
| X20 |
- 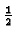 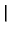 x - x x - x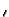 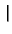 -
- 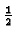 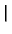 x + x x + x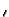 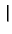 |
| X30 |
- 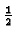 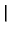 x - x x - x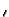 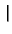 +
+ 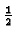 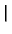 x + x x + x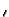  + k/h
+ k/h |


Next: Radial-Cylindrical Coordinates. Steady 1-D.
Up: Laplace Equation. Steady Heat
Previous: Pseudo GF. Rectangular coordinate,
Kevin D. Cole
2002-12-31
![]() < x <
< x < ![]() , 0 < y < W) and the boundary conditions are
, 0 < y < W) and the boundary conditions are
![]() , norm
Ny, and kernel function Pn, as follows:
, norm
Ny, and kernel function Pn, as follows: 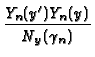 Pn(x, x
Pn(x, x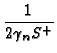
![]() 0, strip and semi-strip.
0, strip and semi-strip.