

Next: Laplace Equation. Steady Heat
Up: Radial-spherical coordinates. Transient 1-D.
Previous: Solid Sphere, transient 1-D.
RS11 Hollow sphere, a < r < b, with G = 0 (Dirichlet) at r = a and G = 0 (Dirichlet) at r = b.
a. Best convergence for (t - 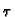 ) small:
) small:
GRS11(r, t 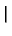 r r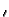 , ,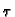
 ) ) |
= |
![$\displaystyle {\frac{1}{8\pi
r\,r^{\prime }[\pi \alpha (t-\tau )]^{1/2}}}$](img314.gif) 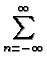 ![$\displaystyle \left\{\vphantom{ \exp \left[ -\frac{[2n(b-a)+r-r^{\prime }]^{2}}{4\alpha (t-\tau )}%
\right] }\right.$](img379.gif) exp exp![$\displaystyle \left[\vphantom{ -\frac{[2n(b-a)+r-r^{\prime }]^{2}}{4\alpha (t-\tau )}%
}\right.$](img380.gif) -
- ![$\displaystyle {\frac{[2n(b-a)+r-r^{\prime }]^{2}}{4\alpha (t-\tau )}}$](img381.gif)
![$\displaystyle \left.\vphantom{ -\frac{[2n(b-a)+r-r^{\prime }]^{2}}{4\alpha (t-\tau )}%
}\right]$](img382.gif)
![$\displaystyle \left.\vphantom{ \exp \left[ -\frac{[2n(b-a)+r-r^{\prime }]^{2}}{4\alpha (t-\tau )}%
\right] }\right.$](img383.gif) |
|
| |
|
![$\displaystyle \left.\vphantom{ +\exp \left[ -\frac{[2n(b-a)+r+r^{\prime }-2a)^{2}}{4\alpha (t-\tau
)}\right] }\right.$](img384.gif) +exp
+exp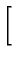 -
- 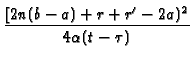
![$\displaystyle \left.\vphantom{ -\frac{[2n(b-a)+r+r^{\prime }-2a)^{2}}{4\alpha (t-\tau
)}}\right]$](img387.gif)
![$\displaystyle \left.\vphantom{ +\exp \left[ -\frac{[2n(b-a)+r+r^{\prime }-2a)^{2}}{4\alpha (t-\tau
)}\right] }\right\}$](img388.gif) |
|
b. Best convergence for (t - 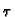 ) large:
) large:
GRS11(r, t 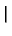 r r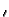 , ,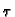
 ) ) |
= |
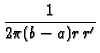 |
|
| |
|
x 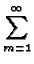 exp exp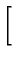 -
- 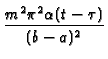
![$\displaystyle \left.\vphantom{ -\frac{m^{2}\pi ^{2}\alpha (t-\tau )%
}{(b-a)^{2}}}\right]$](img392.gif) sin(m sin(m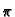 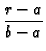 )sin(m )sin(m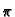 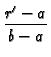 ) ) |
|
RS12 Hollow sphere, a < r < b, with G = 0 (Dirichlet) at r = a and
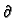 G/
G/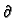 r = 0 (Neumann) at r = b.
r = 0 (Neumann) at r = b.
a. Best convergence for
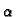 (t -
(t - 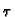 )/(b - a)2 < 0.022:
)/(b - a)2 < 0.022:
GRS12(r, t 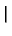 r r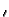 , ,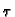
 ) ) |
= |
![$\displaystyle {\frac{1}{8\pi
r\,r^{\prime }[\pi \alpha (t-\tau )]^{1/2}}}$](img314.gif) ![$\displaystyle \left\{\vphantom{ \exp \left[ -\frac{(r-r^{\prime })^{2}}{4\alpha (t-\tau )}\right]
}\right.$](img395.gif) exp exp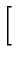 -
- 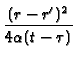
![$\displaystyle \left.\vphantom{ -\frac{(r-r^{\prime })^{2}}{4\alpha (t-\tau )}}\right]$](img325.gif)
![$\displaystyle \left.\vphantom{ \exp \left[ -\frac{(r-r^{\prime })^{2}}{4\alpha (t-\tau )}\right]
}\right.$](img396.gif) |
|
| |
|
![$\displaystyle \left.\vphantom{ -\exp \left[ -\frac{(r+r^{\prime }-2a)^{2}}{4\al...
... +\exp \left[ -\frac{(2b-r-r^{\prime })^{2}}{4\alpha (t-\tau )}\right]
}\right.$](img397.gif) -exp
-exp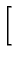 -
- 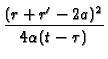
![$\displaystyle \left.\vphantom{ -\frac{(r+r^{\prime }-2a)^{2}}{4\alpha (t-\tau )}%
}\right]$](img399.gif) + exp
+ exp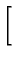 -
- 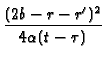
![$\displaystyle \left.\vphantom{ -\frac{(2b-r-r^{\prime })^{2}}{4\alpha (t-\tau )}}\right]$](img401.gif)
![$\displaystyle \left.\vphantom{ -\exp \left[ -\frac{(r+r^{\prime }-2a)^{2}}{4\al...
...+\exp \left[ -\frac{(2b-r-r^{\prime })^{2}}{4\alpha (t-\tau )}\right]
}\right\}$](img402.gif) |
|
| |
|
- 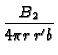 exp exp B2 B2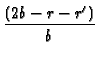 + B22
+ B22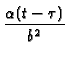
![$\displaystyle \left.\vphantom{ B_{2}\frac{(2b-r-r^{\prime
})}{b^{{}}}+B_{2}^{2}\frac{\alpha (t-\tau )}{b^{2}}}\right]$](img405.gif) |
|
| |
|
x erfc![$\displaystyle \left[\vphantom{ \frac{2b-r-r^{\prime }}{[4\alpha (t-\tau )]^{1/2}}%
+\frac{B_{2}\left[ \alpha (t-\tau )\right] ^{1/2}}{b^{{}}}}\right.$](img371.gif) ![$\displaystyle {\frac{2b-r-r^{\prime }}{[4\alpha (t-\tau )]^{1/2}}}$](img372.gif) +
+ ![$\displaystyle {\frac{B_{2}\left[ \alpha (t-\tau )\right] ^{1/2}}{b^{{}}}}$](img373.gif)
![$\displaystyle \left.\vphantom{ \frac{2b-r-r^{\prime }}{[4\alpha (t-\tau )]^{1/2}}%
+\frac{B_{2}\left[ \alpha (t-\tau )\right] ^{1/2}}{b^{{}}}}\right]$](img374.gif) |
|
b. Best convergence for (t - 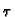 ) large:
) large:
GRS12(r, t  r r , ,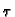
 ) ) |
= |
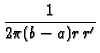 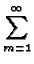 exp exp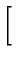 -
- 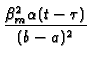
![$\displaystyle \left.\vphantom{ -\frac{\beta
_{m}^{2}\alpha (t-\tau )}{(b-a)^{2}}}\right]$](img408.gif) |
|
| |
|
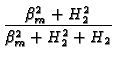 sin( sin(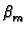 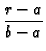 )sin( )sin(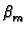 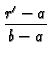 ) ) |
|
where the eigenvalues are given by positive roots of
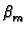 cot cot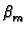 = - H2
= - H2 |
|
and where
H2 = B2R2; B2 = - 1; R2 = (b - a)/b.
RS13 Hollow sphere, a < r < b, with G = 0 (Dirichlet) at r = a and
k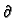 G/
G/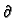 r + hG = 0 (convection) at r = b.
r + hG = 0 (convection) at r = b.
a. Best convergence for
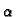 (t -
(t - 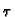 )/(b - a)2 < 0.022
(note
B2 = h2b/k - 1):
)/(b - a)2 < 0.022
(note
B2 = h2b/k - 1):
GRS13(r, t 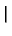 r r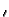 , ,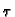
 ) ) |
= |
![$\displaystyle {\frac{1}{8\pi
r\,r^{\prime }[\pi \alpha (t-\tau )]^{1/2}}}$](img314.gif) ![$\displaystyle \left\{\vphantom{ \exp \left[ -\frac{(r-r^{\prime })^{2}}{4\alpha (t-\tau )}\right]
}\right.$](img395.gif) exp exp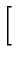 -
- 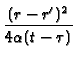
![$\displaystyle \left.\vphantom{ -\frac{(r-r^{\prime })^{2}}{4\alpha (t-\tau )}}\right]$](img325.gif)
![$\displaystyle \left.\vphantom{ \exp \left[ -\frac{(r-r^{\prime })^{2}}{4\alpha (t-\tau )}\right]
}\right.$](img396.gif) |
|
| |
|
![$\displaystyle \left.\vphantom{ -\exp \left[ -\frac{(r+r^{\prime }-2a)^{2}}{4\al...
... +\exp \left[ -\frac{(2b-r-r^{\prime })^{2}}{4\alpha (t-\tau )}\right]
}\right.$](img397.gif) -exp
-exp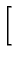 -
- 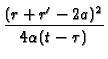
![$\displaystyle \left.\vphantom{ -\frac{(r+r^{\prime }-2a)^{2}}{4\alpha (t-\tau )}%
}\right]$](img399.gif) + exp
+ exp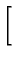 -
- 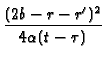
![$\displaystyle \left.\vphantom{ -\frac{(2b-r-r^{\prime })^{2}}{4\alpha (t-\tau )}}\right]$](img401.gif)
![$\displaystyle \left.\vphantom{ -\exp \left[ -\frac{(r+r^{\prime }-2a)^{2}}{4\al...
...+\exp \left[ -\frac{(2b-r-r^{\prime })^{2}}{4\alpha (t-\tau )}\right]
}\right\}$](img402.gif) |
|
| |
|
- 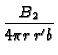 exp exp B2 B2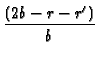 + B22
+ B22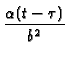
![$\displaystyle \left.\vphantom{ B_{2}\frac{(2b-r-r^{\prime
})}{b^{{}}}+B_{2}^{2}\frac{\alpha (t-\tau )}{b^{2}}}\right]$](img405.gif) |
|
| |
|
x erfc![$\displaystyle \left[\vphantom{ \frac{2b-r-r^{\prime }}{[4\alpha (t-\tau )]^{1/2}}%
+\frac{B_{2}\left[ \alpha (t-\tau )\right] ^{1/2}}{b^{{}}}}\right.$](img371.gif) ![$\displaystyle {\frac{2b-r-r^{\prime }}{[4\alpha (t-\tau )]^{1/2}}}$](img372.gif) +
+ ![$\displaystyle {\frac{B_{2}\left[ \alpha (t-\tau )\right] ^{1/2}}{b^{{}}}}$](img373.gif)
![$\displaystyle \left.\vphantom{ \frac{2b-r-r^{\prime }}{[4\alpha (t-\tau )]^{1/2}}%
+\frac{B_{2}\left[ \alpha (t-\tau )\right] ^{1/2}}{b^{{}}}}\right]$](img374.gif) |
|
b. Best convergence for (t - 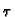 ) large:
) large:
GRS13(r, t 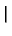 r r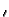 , ,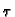
 ) ) |
= |
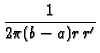 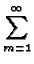 exp exp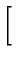 -
- 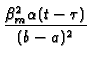
![$\displaystyle \left.\vphantom{ -\frac{\beta
_{m}^{2}\alpha (t-\tau )}{(b-a)^{2}}}\right]$](img408.gif) |
|
| |
|
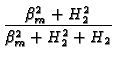 sin( sin(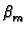 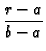 )sin( )sin(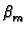 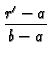 ) ) |
|
where the eigenvalues are given by positive roots of
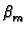 cot cot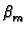 = - H2
= - H2 |
|
and where
H2 = B2R2; B2 = h2b/k - 1; R2 = (b - a)/b.


Next: Laplace Equation. Steady Heat
Up: Radial-spherical coordinates. Transient 1-D.
Previous: Solid Sphere, transient 1-D.
Kevin D. Cole
2002-12-31
![$\displaystyle {\frac{1}{8\pi
r\,r^{\prime }[\pi \alpha (t-\tau )]^{1/2}}}$](img314.gif)
![$\displaystyle {\frac{[2n(b-a)+r-r^{\prime }]^{2}}{4\alpha (t-\tau )}}$](img381.gif)
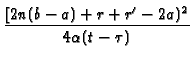
![$\displaystyle {\frac{1}{8\pi
r\,r^{\prime }[\pi \alpha (t-\tau )]^{1/2}}}$](img314.gif)
![$\displaystyle {\frac{[2n(b-a)+r-r^{\prime }]^{2}}{4\alpha (t-\tau )}}$](img381.gif)
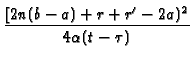
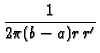
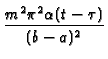
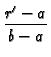 )
)![$\displaystyle {\frac{1}{8\pi
r\,r^{\prime }[\pi \alpha (t-\tau )]^{1/2}}}$](img314.gif)
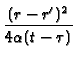
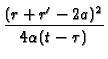
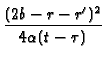
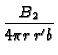 exp
exp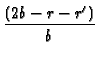 + B22
+ B22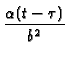
![$\displaystyle {\frac{2b-r-r^{\prime }}{[4\alpha (t-\tau )]^{1/2}}}$](img372.gif) +
+ ![$\displaystyle {\frac{B_{2}\left[ \alpha (t-\tau )\right] ^{1/2}}{b^{{}}}}$](img373.gif)
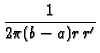
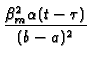
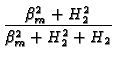 sin(
sin(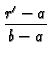 )
)![]() G/
G/![]() r + hG = 0 (convection) at r = b.
r + hG = 0 (convection) at r = b.
![]() (t -
(t - ![]() )/(b - a)2 < 0.022
(note
B2 = h2b/k - 1):
)/(b - a)2 < 0.022
(note
B2 = h2b/k - 1):
![$\displaystyle {\frac{1}{8\pi
r\,r^{\prime }[\pi \alpha (t-\tau )]^{1/2}}}$](img314.gif)
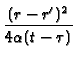
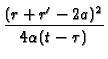
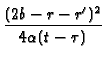
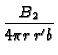 exp
exp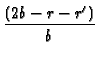 + B22
+ B22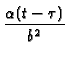
![$\displaystyle {\frac{2b-r-r^{\prime }}{[4\alpha (t-\tau )]^{1/2}}}$](img372.gif) +
+ ![$\displaystyle {\frac{B_{2}\left[ \alpha (t-\tau )\right] ^{1/2}}{b^{{}}}}$](img373.gif)
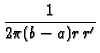
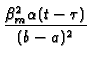
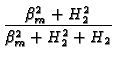 sin(
sin(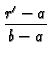 )
)